Why Mathematical Modeling for FMD
- ✓Understand disease dynamics: Models describe how FMD spreads between animals, herds, and regions, capturing transmission rate, incubation, carrier animals, and seasonality.
- ✓Evaluate control strategies: Test impacts of vaccination frequency/coverage, culling, and movement restrictions.
- ✓Real-world example: Biannual vaccination campaigns in India were designed and monitored with modeling insights.
- ✓Optimize resource use: Guide allocation of vaccines, manpower, and funds; target high-risk zones to reduce wastage.
- ✓Policy & decision support: Provide evidence for eradication programs and progress toward FMD-free zones for livestock trade.
- ✓Assess vaccination effectiveness: Quantify herd immunity and evaluate whether frequency and coverage prevent outbreaks.
- ✓Simulate “what-if” scenarios: Explore outcomes under varying vaccination levels and movement controls without real-world risk.
Featured: Modeling Foot-and-Mouth Disease (FMD) Across Hosts
This section summarizes your FMD focus—integrating vaccination and isolation of infected animals as primary control measures—while remaining part of a general portal.
Objective
Develop a mathematical model for FMD dynamics in multi-host systems (cattle, buffalo, sheep/goats, pigs as amplifiers) with vaccination and isolation integrated as policy levers.
Key Questions the Model Can Answer
- What drives outbreak speed, peak, and size, and which parameters (β, recovery, immunity, vaccination, rainfall/temperature/pH) are most influential?
- Which combinations and timings of vaccination, quarantine, and isolation minimize epidemic impact and disruption?
- How can we estimate introduction risk, forecast long-term dynamics, and plan to prevent future waves?
Assumptions (Deterministic SEIR-style Model)
- Homogeneous mixing within modeled units.
- Deterministic dynamics (no stochastic noise in baseline).
- Constant rates for birth, death, recovery within scenarios.
- Equal susceptibility and infectiousness within a compartment.
- Focus on conditions for epidemic takeoff vs. endemic persistence.
FMD Model Overview
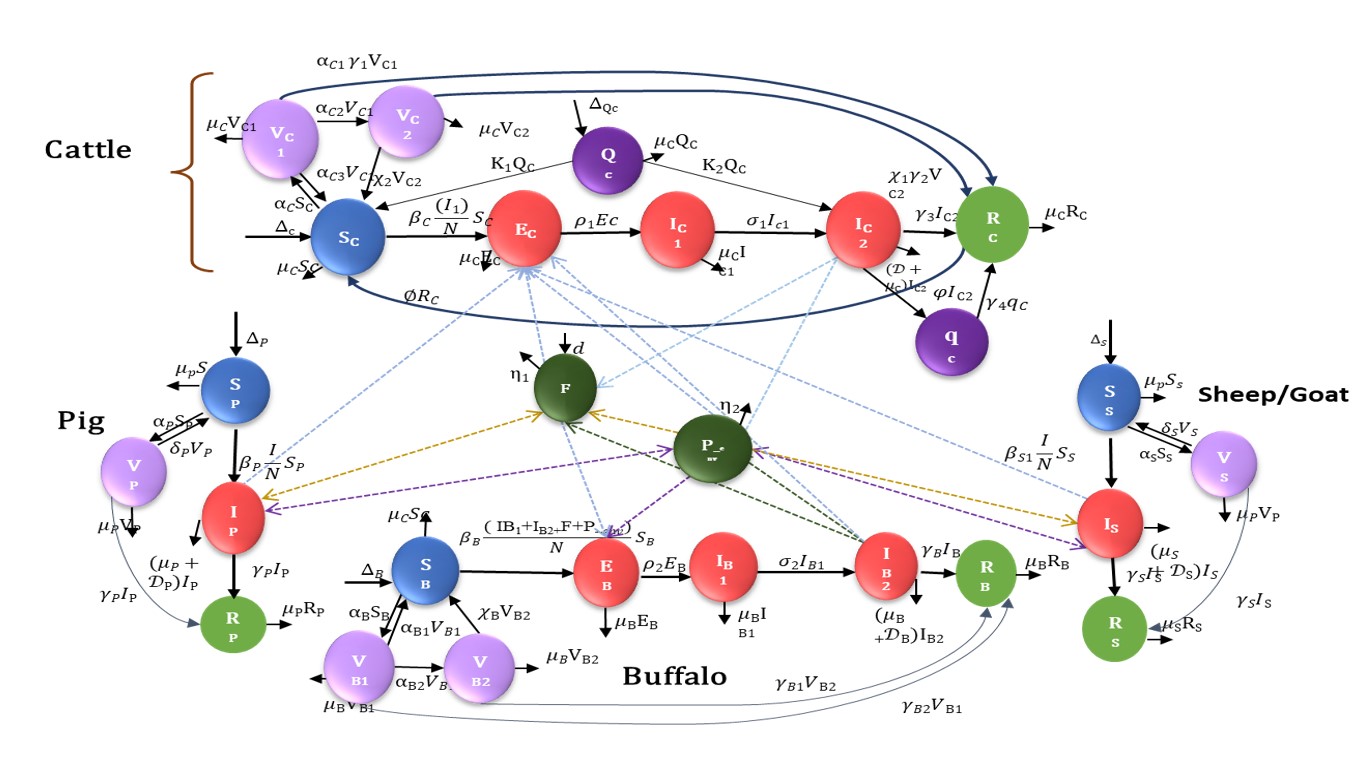
Flows K1, K2 denote quarantine-related transitions; f_env scales environment/fomite-mediated spillover.
Cattle (SEIRVQq)
$\displaystyle \begin{aligned} \frac{dS_C}{dt} &= \Delta_C + \alpha_{C3} V_{C1} + \chi''_{2} V_{C2} + K_1 Q_C + \varnothing R_C \\ &\quad - \Big[ \alpha_C + \mu_C + \beta_C \frac{I_{C1}+I_{C2}+I_{B2} + f_{env} I_P + f_{env} I_S}{N} \Big] S_C, \\ \frac{dE_C}{dt} &= \beta_C \frac{I_{C1}+I_{C2}+I_{B2} + f_{env} I_P + f_{env} I_S}{N} S_C - (\rho_1+\mu_C) E_C, \\ \frac{dI_{C1}}{dt} &= \rho_1 E_C - (\mu_C+\sigma_1) I_{C1}, \\ \frac{dI_{C2}}{dt} &= \sigma_1 I_{C1} + K_2 Q_C - (\gamma_3+\mu_C+\varphi + D_C) I_{C2}, \\ \frac{dR_C}{dt} &= \alpha_{C1}\gamma_1 V_{C1} + \chi_1 \gamma_2 V_{C2} + \gamma_3 I_{C2} + \gamma_4 q_C - (\mu_C+\varnothing) R_C, \\ \frac{dV_{C1}}{dt} &= \alpha_C S_C - (\alpha_{C1}\gamma_1 + \alpha_{C2} + \alpha_{C3} + \mu_C) V_{C1}, \\ \frac{dV_{C2}}{dt} &= \alpha_{C2} V_{C1} - (\chi_1\gamma_2 + \mu_C + \chi''_{2}) V_{C2}, \\ \frac{dQ_C}{dt} &= \Delta_{QC} - (K_1 + K_2 + \mu_C) Q_C, \\ \frac{d q_C}{dt} &= \varphi I_{C2} - (\gamma_4 + \mu_C) q_C. \end{aligned} $
Buffalo (SEIRV)
$\displaystyle \begin{aligned} \frac{dS_B}{dt} &= \Delta_B + \alpha_{B1} V_{B1} + \chi_B V_{B2} - \Big[ \alpha_B + \mu_B + \beta_B \frac{I_{B1}+I_{B2} + f_{env}\,F\,I_{C2}}{N} \Big] S_B, \\ \frac{dE_B}{dt} &= \beta_B \frac{I_{B1}+I_{B2} + f_{env}\,F\,I_{C2}}{N} S_B - (\rho_2 + \mu_B) E_B, \\ \frac{dI_{B1}}{dt} &= \rho_2 E_B - (\mu_B+\sigma_2) I_{B1}, \\ \frac{dI_{B2}}{dt} &= \sigma_2 I_{B1} - (\mu_B + D_B) I_{B2}, \\ \frac{dV_{B1}}{dt} &= \alpha_B S_B - (\alpha_{B1} + \alpha_{B2} + \mu_B) V_{B1} - \gamma_{B2} V_{B1}, \\ \frac{dV_{B2}}{dt} &= \alpha_{B2} V_{B1} - (\mu_B + \chi_B) V_{B2} - \gamma_{B1} V_{B2}, \\ \frac{dR_B}{dt} &= \gamma_B I_B - \mu_B R_B + \gamma_{B1} V_{B2} + \gamma_{B2} V_{B1}. \end{aligned} $
Sheep/Goat (SVIR)
$\displaystyle \begin{aligned} \frac{dS_S}{dt} &= \Delta_S + \delta_S V_S - \big[ \beta_S \frac{I_S}{N} + \mu_S + \alpha_S \big] S_S, \\ \frac{dI_S}{dt} &= \beta_S \frac{I_S}{N} S_S - (\mu_S + D_S) I_S, \\ \frac{dV_S}{dt} &= \alpha_S S_S - (\delta_S + \mu_S) V_S - \gamma_{S1} V_S, \\ \frac{dR_S}{dt} &= \gamma_S I_S - \mu_S R_S + \gamma_{S1} V_S. \end{aligned} $
Pig (SVIR)
$\displaystyle \begin{aligned} \frac{dS_P}{dt} &= \Delta_P + \delta_P V_P - \big[ \beta_P \frac{I_P}{N} + \mu_P + \alpha_P \big] S_P, \\ \frac{dI_P}{dt} &= \beta_P \frac{I_P}{N} S_P - (\mu_P + D_P) I_P, \\ \frac{dV_P}{dt} &= \alpha_P S_P - (\delta_P + \mu_P) V_P - \gamma_{P1} V_P, \\ \frac{dR_P}{dt} &= \gamma_P I_P - \mu_P R_P + \gamma_{P1} V_P. \end{aligned} $
Model Parameterization
| Sl. No | Parameter | Description |
|---|---|---|
| 1 | β_C | Transmission rate of cattle |
| 2 | β_B | Transmission rate of buffalo |
| 3 | β_P | Transmission rate of pig |
| 4 | β_S | Transmission rate of sheep/goat |
| 5 | μ_C | Death rate of cattle |
| 6 | μ_B | Death rate of buffalo |
| 7 | μ_P | Death rate of pig |
| 8 | D_C | Disease-induced mortality rate (cattle) |
| 9 | ρ_1 | Exposed cattle → subclinical infected (rate) |
| 10 | σ_1 | Subclinical → clinical cattle (rate) |
| 11 | ρ_2 | Exposed buffalo → infected buffalo (rate) |
| 12 | σ_2 | Subclinical → clinical buffalo (rate) |
| 13 | ∅ | Loss of immunity (1/180 days for 6-month average) |
| 14 | α_C | Vaccination rate of cattle |
| 15 | α_B | Vaccination rate of buffalo |
| 16 | φ | Isolation (symptomatic cattle) rate |
| 17 | χ_2 | Waning rate of vaccinated animals (general) |
| 18 | γ_3 | Recovery rate of symptomatic infected (cattle) |
| 19 | γ_4 | Recovery rate of isolated cattle |
| 20 | χ''_2 | Waning rate of vaccinated cattle (V_C2) |
| 21 | η_1 | Fomites pathogen decay rate |
| 22 | η_2 | Environment pathogen decay rate |
| 23 | S_C | Susceptible cattle |
| 24 | E_C | Exposed/latent cattle |
| 25 | I_C1 | Subclinical infectious cattle |
| 26 | I_C2 | Clinical infectious cattle |
| 27 | R_C | Recovered cattle |
| 28 | V_C1 | Vaccinated (fewer rounds) cattle |
| 29 | V_C2 | Vaccinated (more rounds) cattle |
| 30 | Q_C | Quarantined cattle |
| 31 | q_C | Isolated cattle |
| 32 | S_B | Susceptible buffalo |
| 33 | E_B | Exposed buffalo |
| 34 | I_B1 | Subclinical infected buffalo |
| 35 | I_B2 | Clinical infected buffalo |
| 36 | R_B | Recovered buffalo |
| 37 | V_B1 | Vaccinated (fewer rounds) buffalo |
| 38 | V_B2 | Vaccinated (more rounds) buffalo |
| 39 | S_P | Susceptible pigs |
| 40 | V_P | Vaccinated pigs |
| 41 | I_P | Infected pigs |
| 42 | R_P | Recovered pigs |
| 43 | S_S | Susceptible sheep/goats |
| 44 | V_S | Vaccinated sheep/goats |
| 45 | I_S | Infected sheep/goats |
| 46 | R_S | Recovered sheep/goats |
| 47 | Δ_C | Recruitment/births to S_C |
| 48 | Δ_B | Recruitment/births to S_B |
| 49 | Δ_P | Recruitment/births to S_P |
| 50 | Δ_S | Recruitment/births to S_S |
| 51 | K_1 | Quarantine flow (e.g., Q_C → S_C) |
| 52 | K_2 | Quarantine flow (e.g., Q_C → I_C2) |
| 53 | Δ_QC | Inflow into quarantine (Q_C) |
| 54 | D_B | Disease-induced mortality (buffalo) |
| 55 | D_P | Disease-induced mortality (pig) |
| 56 | D_S | Disease-induced mortality (sheep/goat) |
| 57 | α_S | Vaccination rate of sheep/goat |
| 58 | α_P | Vaccination rate of pig |
| 59 | μ_S | Death rate of sheep/goat |
| 60 | δ_S | Waning from vaccinated to susceptible (S/G) |
| 61 | δ_P | Waning from vaccinated to susceptible (pig) |
| 62 | γ_S | Recovery rate (sheep/goat) |
| 63 | γ_{S1} | Vaccine-take/maturation (V_S → R_S) |
| 64 | γ_P | Recovery rate (pig) |
| 65 | γ_{P1} | Vaccine-take/maturation (V_P → R_P) |
| 66 | γ_B | Recovery rate (buffalo) |
| 67 | γ_{B1}, γ_{B2} | Auxiliary vaccine-related transitions (buffalo) |
| 68 | f_{env} | Environment/fomite-mediated transmission scaling |
| 69 | F | Fomite contamination index |
| 70 | N | Total population (all relevant hosts) |
